Neste artigo você verá:
Contexto Geral do MEF.
Parece razoável afirmar que o método dos elementos finitos vem revolucionando a forma como os engenheiros conduzem os projetos de engenharia em todo o mundo. Houve, a partir da década de 1960, um extenso crescimento no desenvolvimento deste método, no qual passou a ser implementado gradativamente na rotina dos grupos de engenharia desde então (veja este artigo do prof Clough sobre a história do MEF) . Esse fato foi decisivo no avanço de diversos setores da indústria, em especial aquelas de grande responsabilidade, no qual podemos destacar a indústria nuclear e a indústria aeroespacial, no contexto da guerra fria. Naquela época, as limitações tecnológicas faziam com que as análises se limitassem a poucos problemas e, de modo geral, muito simplificados devido às demandas de processamento. Essa realidade era restrita a pequenos grupos que possuíam altos investimentos. Contudo, mas últimas décadas, com a expansão e o barateamento dos processadores, facilitou-se o acesso às ferramentas de simulação pelo método dos elementos finitos, de tal modo que, atualmente, estas sejam facilmente encontradas nas empresas de engenharia, desde aquelas com altos orçamentos, como também pequenos escritórios de projeto e até mesmo profissionais liberais.
Essa facilidade trouxe consigo uma relação contraditória entre a usabilidade do software e o conhecimento acerca do MEF (como chamamos o método dos elementos finitos). Ou seja, quanto mais os softwares de CAE (engenharia assistida por computador) se tornam amigáveis ao usuário, menos conhecimento técnico sobre o MEF é necessário para sua manipulação, o que, por vezes, pode induzir o analista com pouca ou nenhuma experiência, à crença de que a análise consiste apenas no manuseio do software, sem o respectivo conhecimento do método. Esse fato gera, por vezes, análises cujos resultados são questionáveis e até inconsistentes, situação que é agravada quando o problema exige conhecimento de tópicos mais avançados, com modelos não lineares e/ou tópicos pouco comuns, por exemplo.

Como Funciona o Método dos Elementos Finitos?
A resposta para esta pergunta pode ser simples ou complexa. Admitindo que não há muito espaço para aprofundamento neste artigo, vamos à resposta simples: o método dos elementos finitos é nada mais que uma estratégia matemática para a obtenção de soluções de problemas complexos, expressos em domínios contínuos, a partir da combinação de soluções simples obtidas do particionamento deste domínio em um número finito de subdomínios (os subdomínios são os elementos finitos!).
Para esclarecer essa ideia, observe as imagens abaixo:
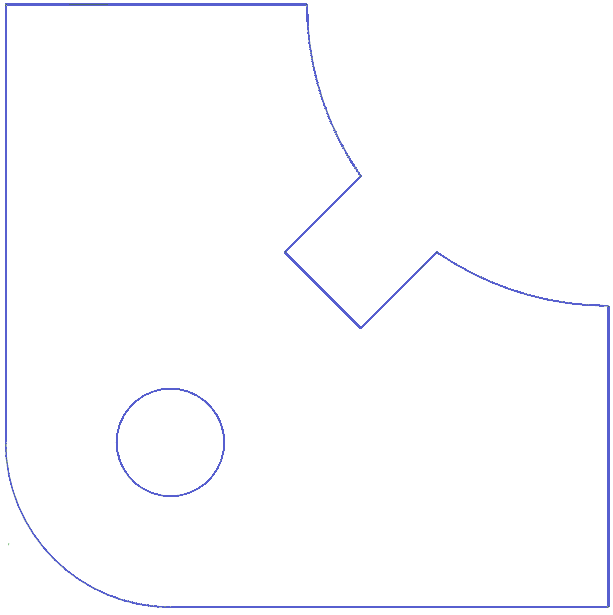
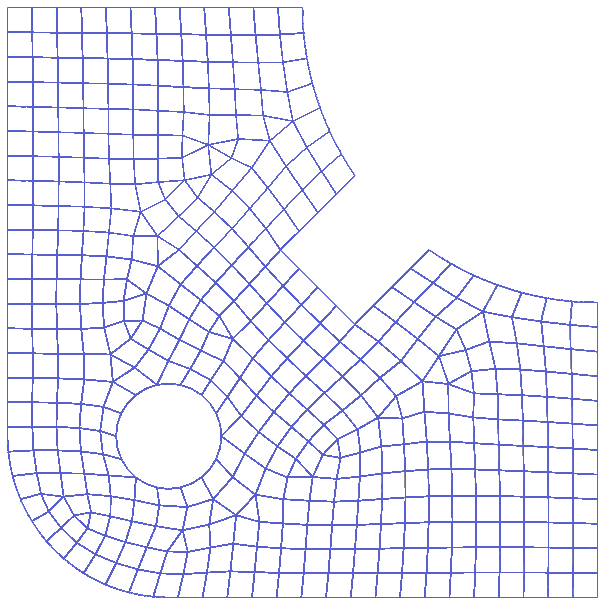
Elas ilustram bem o princípio fundamental do Método dos Elementos Finitos, citado acima. Na figura 2(A), há uma peça de domínio contínuo, cuja solução é de difícil estabelecimento (e, muitas vezes, até impossível!). Contudo, discretizando-se o sólido em um número finito de partes simples (e daí o nome de elementos finitos), como na figura 2(B), podemos estabelecer a solução para cada uma destas partes simples (Figura 3). Assim, combinando todas as partes adequadamente, conseguimos a solução do todo.
O que o MEF Tem de Tão Especial?
Refletindo sobre esta estratégia, percebe-se que ela é similar àquelas utilizadas em tantos outros métodos estudados nos cursos de cálculo numérico nas faculdades das ciências exatas, como a regra de Simpson para integração, por exemplo).
Em primeiro lugar, deve estar claro que o método dos elementos finitos é um método utilizado para a solução de sistemas de equações diferenciais parciais, comumente encontrado em diversos problemas da física. Como exemplo, observe as equações de equilíbrio estático de um sólido plano deformável abaixo:
\[
\begin{aligned}
\frac{\partial{\sigma_{xx}}}{\partial{x}} + \frac{\partial{\tau_{yx}}}{\partial{y}} = f_x \\
\frac{\partial{\tau_{xy}}}{\partial{x}} + \frac{\partial{\sigma_{yy}}}{\partial{y}} = f_y
\end{aligned}
\tag{Eq.1} \label{eq:momentum}
\]
O sucesso do MEF é, em sua imensa parte, devido à sua versatilidade, apresentando resultados confiáveis para problemas de diversos níveis de complexidade, tanto complexidade geométrica quanto de condições de contorno, além da possibilidade de integração entre diferentes disciplinas, e que foi impulsionado pelo avanço da indústria de processadores que favoreceu sua aplicabilidade, como mencionado no início deste artigo.
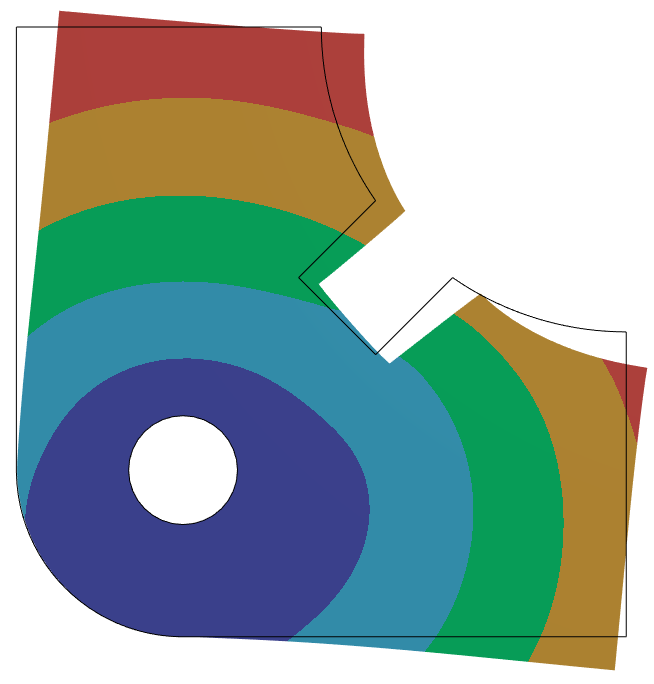
As equações \eqref{eq:momentum} são válidas em todos os pontos do domínio estudado, contudo, é exatamente este fato que apresenta a maior dificuldade na determinação da solução das equações. Portanto, o primeiro passo é a transformação das equações numa forma integral, em que a solução é válida, não em todos os pontos, mas em termos médios do domínio. Do ponto de vista prático, a solução é dada em pontos específicos chamados de nós, em que correspondem às arestas dos elementos finitos, como pode ser visto na imagem abaixo.
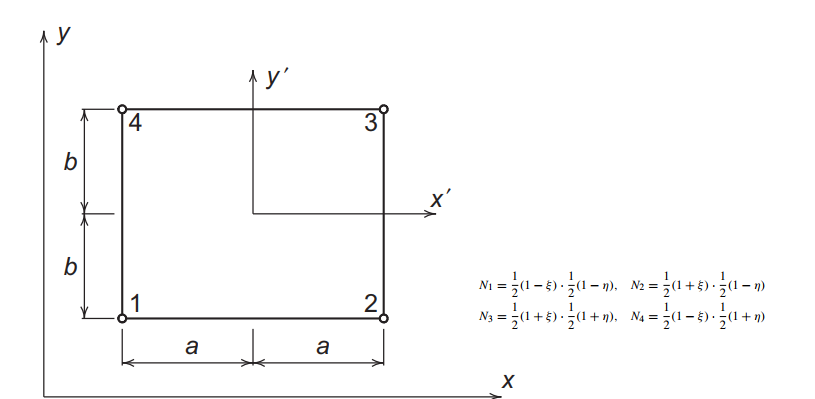
Aplicando o MEF.
Em posse das equações em sua forma fraca, usa-se de funções de interpolação para descrever as variáveis que dominam o fenômeno estudado para se obter a solução. Por exemplo, no caso das equações acima, poderíamos escrever os deslocamentos como combinação de diversas funções – será usado um problema unidimensional por questões didáticas. Lembrando que tensões, deformações e deslocamentos possuem uma relação matemática conhecida, a equação (1) pode ser reescrita na forma:
como \(\hspace{0.5cm}\sigma = D*\epsilon\) e \(\hspace{2cm} \epsilon_{x}=\frac{\partial{u}}{\partial{x}}\hspace{2cm}\)
então, das equações \eqref{eq:momentum}:
$$\hspace{1cm}\frac{\partial}{\partial{x}}{(E*\frac{\partial{u}}{\partial{x}})}=\vec{f}$$
Sendo \(D\) a relação constitutiva que associa as tensões com as deformações, se tratarmos de problemas unidimensional, \(D\) é o módulo de elasticidade \(E\).
Realizando uma série de transformações nas equações e colocando-as na forma integral, chegamos à seguinte relação:
$$\int_{V}{\left(\frac{\partial{u}}{\partial{x}}\right)E\left(\frac{\partial{u}}{\partial{x}}\right)} dV= \int_{S}{fdS}\tag{eq. (2)}$$Além disso, os deslocamentos podem ser escritos como uma combinação linear de N funções de interpolação (essa estratégia vem dos métodos dos resíduos ponderados, mais precisamente do método de Galerkin):
$$\bar{u} = \sum_{k=1}^{N}{h(x){(k)}*u{(k)}}$$
Ainda sobre as funções de interpolação, há algumas observações a serem feitas. A primeira é que, de modo geral, elas são polinomiais de ordem 1 ou 2 (podendo ser de ordens superiores, e até mesmo com outras formas, mas na prática cotidiana não é comum). Além disso, cada problema exige que as funções satisfaçam determinadas características que, em resumo, devem ser capazes de descrever o fenômeno físico que está sendo modelado. Por exemplo, se os deslocamentos num determinado tipo de carregamento tem comportamento parabólico, usar uma função de primeiro grau \((h(x)=ax+b)\) pode não ser muito adequado.
Uma vez que se conhece as funções de interpolação \(h(x)\), viabiliza-se a solução do problema individual de cada elemento e permite-se generalizar a solução do todo a partir da sobreposição das soluções individuais. Destaco que há diversas etapas intermediárias que foram omitidas por esse se tratar de um espaço limitado para alguns detalhes mais aprofundados.
Realizando as derivadas de \(\bar{u}\) em relação à \(x\) e substituindo na eq(2), chega-se a seguinte expressão:
$$[K]{u}={f}$$
$$[K] = A\int_{x}{(B^T)E(B)dx}$$
Com \(A\) sendo a área da seção transversal do elemento 1D e \(B\) a matriz que opera sobre os deslocamentos para cálculo das deformações. Chegamos portanto na expressão da matriz de rigidez do elemento finito. Assim, resolvendo o sistema de equações lineares, fazendo \(u=K^{-1}f\), chega-se a solução do problema da eq.(1).
Outro detalhe importante do MEF é o aspecto computacional. Ao tratarmos o sistema de equações (1) através da discretização do domínio, o problema passa a ter uma estrutura matricial e, portanto, adequado para processamento no computador. Este ponto é de suma importância para o entendimento da relação entre modelagem e desempenho no computador. É natural do processo de modelagem que se faça simplificações no problema com o objetivo de adequá-lo para o poder de processamento disponível. Ou seja, detalhes muito pequeno que não são de interesse da análise podem ser desprezados sem prejuízos para o estudo a ser realizado. Por outro lado, caso seja inserido no modelo todos os detalhes, é provável que haja uma demanda computacional muito superior ao caso anterior, por vezes comprometendo a viabilidade da análise.
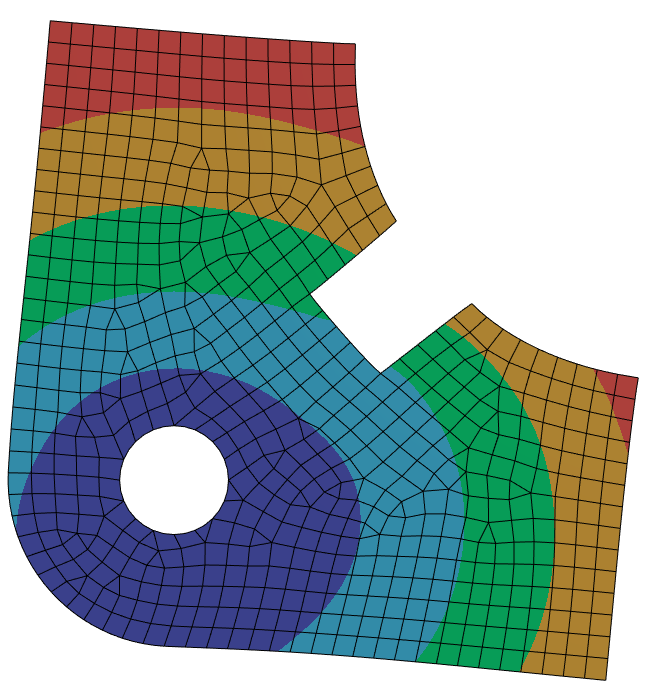
Aplicações e Limitações do Método dos Elementos Finitos.
O Método dos Elementos Finitos se consolidou como uma ferramenta essencial em muitas indústrias devido à sua capacidade de reduzir custos associados a testes físicos. Ele permite que projetos sejam analisados detalhadamente antes de sua construção, antecipando comportamentos e prevenindo falhas. Embora o MEF não substitua completamente os testes físicos, ele reduz a quantidade de ensaios necessários para validar um projeto. Dentre as aplicações mais comuns do MEF, podemos citar a construção civil, engenharia naval, aeronáutica e aeroespacial, indústria química, nuclear, óleo e gás, onde o MEF é amplamente empregado para a análise estrutural de elementos sólidos, cascas, vigas e treliças, em que estão presentes análises estáticas, dinâmicas, térmicas, entre outras.
Apesar de o Método dos Elementos Finitos (MEF) ter revolucionado a forma como realizamos análises numéricas em engenharia, ele não é uma ferramenta adequada em muitas aplicações, como os exemplos abaixo (mas não se limitando apenas estes):
- Dinâmica de fluidos, em especial com turbulência.
- Problemas que envolvam fluxo de neutrons e outras aplicações da neutrônica.
- Problemas de escoamento que envolvam mudanças de fase.
- Problemas de mecânica da fratura.
As limitações do método pode nos frustrar num primeiro momento, contudo este fato é o motor que conduz a pesquisa e desenvolvimento do método a cada dia. Aliás, foi exatamente esta característica que, nos primórdios da utilização do método, permitiu seu atual desenvolvimento. Assim, atualmente há uma série de propostas de variações e extensões do MEF para contornar os problemas mencionados, além de sua utilização em conjunto com outros método, a exemplo do método dos volumes finitos e do método das diferenças finitas.
Sugestões de Leitura.
Dois livros interessantes para quem quer iniciar ou se aprofundar nos conceitos teóricos do MEF estão listados abaixo.
- Um Primeiro Curso em Elementos Finitos (Fish & Belytschko).
- Concepts and Applications of Finite Element Analysis (Robert. D. Cook).